三角形貴州中考數學題匯總及答案
為了讓大家更加清楚歷年貴州三角形的考法,百分網小編幫大家帶來一份三角形之貴州中考數學題匯總,附有答案,有需要的同學可以看一看,更多內容歡迎關注應屆畢業生網!
一、選擇題
1. (2012貴州貴陽3分)如圖,已知點A、D、C、F在同一條直線上,AB=DE,BC=EF,要使△ABC≌△DEF,還需要添加一個條件是【 】
A.∠BCA=∠F B.∠B=∠E C.BC∥EF D.∠A=∠EDF
【答案】B。
【考點】全等三角形的判定。190187。
【分析】應用全等三角形的判定方法逐一作出判斷:
A、由AB=DE,BC=EF和∠BCA=∠F構成SSA,不符合全等的條件,不能推出△ABC≌△DEF,故本選項錯誤;
B、由AB=DE,BC=EF和∠B=∠E構成SAS,符合全等的條件,能推出△ABC≌△DEF,故本選項正確;
C、∵BC∥EF,∴∠F=∠BCA。
由AB=DE,BC=EF和∠F=∠BCA構成SSA,不符合全等的條件,不能推出△ABC≌△DEF,故本選項錯誤;
D、由AB=DE,BC=EF和∠A=∠EDF構成SSA,不符合全等的條件,不能推出△ABC≌△DEF,故本選項錯誤。故選B。
2. (2012貴州貴陽3分)如圖,在Rt△ABC中,∠ACB=90°,AB的垂直平分線DE交于BC的延長線于F,若∠F=30°,DE=1,則EF的長是【 】
A.3 B.2 C. D.1
【答案】B。
【考點】線段垂直平分線的性質,含30度角的直角三角形的性質,等腰三角形的判定。
【分析】連接AF,
∵DF是AB的垂直平分線,∴AF=BF。
∵FD⊥AB,∴∠AFD=∠BFD=30°,∠B=∠FAB=90°﹣30°=60°。
∵∠ACB=90°,∴∠BAC=30°,∠FAC=60°﹣30°=30°。
∵DE=1,∴AE=2DE=2。
∵∠FAE=∠AFD=30°,∴EF=AE=2。故選B。
3. (2012貴州安順3分)某一時刻,身髙1.6m的小明在陽光下的影長是0.4m,同一時刻同一地點測得某旗桿的影長是5m,則該旗桿的高度是【 】
A. 1.25m B. 10m C. 20m D. 8m
【答案】C。
【考點】相似三角形的應用。
【分析】設該旗桿的高度為xm,
根據題意得,1.6:0.4=x:5,解得x=20(m)。
∴該旗桿的高度是20m。故選C。
4. (2012貴州畢節3分)如圖,△ABC的三個頂點分別在直線a、b上,且a∥b,若∠1=120°,∠2=80°,則∠3的度數是【 】
A.40° B.60° C.80° D.120°
【答案】A。[來源:學科網]
【考點】平行線的性質,三角形的外角性質。
【分析】∵a∥b,∴∠ABC=∠2=80°(兩直線平行,內錯角相等)。
∵∠1=120°,∠3=∠1-∠ABC(三角形的外角等于和它不相鄰的兩內角之和)。
∴∠3=120°-80°=40°(等量代換)。故選A。
5. (2012貴州畢節3分)如圖.在Rt△ABC中,∠A=30°,DE垂直平分斜邊AC,交AB于D,E式垂足,連接CD,若BD=1,則AC的長是【 】
A.2 B.2 C.4 D.4
【答案】A。
【考點】線段垂直平分線的性質,三角形內角和定理,等腰三角形的性質,含30度角的直角三角形的性質,勾股定理。
【分析】∵∠A=30°,∠B=90°,∴∠ACB=180°-30°-90°=60°。
∵DE垂直平分斜邊AC,∴AD=CD。∴∠A=∠ACD=30°。∴∠DCB=60°-30°=30°。
∵BD=1,∴CD=2=AD。∴AB=1+2=3。
在△BCD中,由勾股定理得:CB= 。
在△ABC中,由勾股定理得: 。故選A。
6. (2012貴州黔南4分)如圖,夏季的一天,身高為1.6m的小玲想測量一下屋前大樹的高度,她沿著樹影BA由B到A走去,當走到C點時,她的影子頂端正好與樹的影子頂端重合,測得BC=3.2m,CA=0.8m,于是得出樹的高度為【 】
A.8m B.6.4m C.4.8m D.10m
【答案】A。
【考點】相似三角形的應用。
【分析】因為人和樹均垂直于地面,所以和光線構成的兩個直角三角形相似,
設樹高x米,則 ,即 ,解得,x=8。故選A。
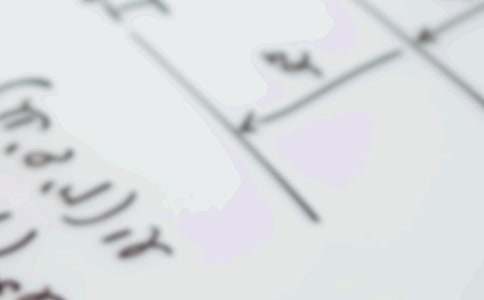
7. (2012貴州黔西南4分)興義市進行城區規劃,工程師需測某樓AB的高度,工程師在D得用高2m的測角儀CD,測得樓頂端A的仰角為30°,然后向樓前進30m到達E,又測得樓頂端A的仰角為60°,樓AB的高為【 】
(A) (B) (C) (D)
8. (2012貴州銅仁4分)如圖,在△ABC中,∠ABC和∠ACB的平分線交于點E,過點E作MN∥BC交AB于M,交AC于N,若BM+CN=9,則線段MN的長為【 】
A.6 B.7 C.8 D.9
【答案】D。
【考點】角平分線的定義,平行線的性質,等腰三角形的判定和性質。
【分析】∵∠ABC、∠ACB的平分線相交于點E,∴∠MBE=∠EBC,∠ECN=∠ECB,
∵MN∥BC,∴∠EBC=∠MEB,∠NEC=∠ECB。∴∠MBE=∠MEB,∠NEC=∠ECN。
∴BM=ME,EN=CN。∴MN=ME+EN,即MN=BM+CN。
∵BM+CN=9∴MN=9。故選D。
9. (2012貴州遵義3分)如圖,在△ABC中,EF∥BC, ,S四邊形BCFE=8,則S△ABC=【 】
A.9 B.10 C.12 D.13
【答案】A。
【考點】相似三角形的判定和性質。
【分析】∵ ,∴ 。
又∵EF∥BC,∴△AEF∽△ABC。∴ 。∴9S△AEF=S△ABC。
又∵S四邊形BCFE=8,∴9(S△ABC﹣8)=S△ABC,解得:S△ABC=9。故選A。
二、填空題
1. (2012貴州安順4分)在一自助夏令營活動中,小明同學從營地A出發,要到A地的北偏東60°方向的C處,他先沿正東方向走了200m到達B地,再沿北偏東30°方向走,恰能到達目的地C(如圖),那么,由此可知,B、C兩地相距 ▲ m.
【答案】200。
【考點】解直角三角形的應用(方向角問題),三角形內角和定理,等腰三角形的判定。
【分析】由已知得:∠ABC=90°+30°=120°,∠BAC=90°﹣60°=30°。
∴∠ACB=180°﹣∠ABC﹣∠BAC=180°﹣120°﹣30°=30°。
∴∠ACB=∠BAC。∴BC=AB=200(m)。
2. (2012貴州安順4分)如圖,∠1=∠2,添加一個條件 ▲ 使得△ADE∽△ACB.
【答案】∠D=∠C(答案不唯一)。
【考點】開放型,相似三角形的判定。
【分析】∵∠1=∠2,∴∠1+∠BAE=∠2+∠BAE,即∠DAE=∠CAB。
∴當∠D=∠C或∠E=∠B或 時,△ADE∽△ACB(答案不唯一)。
3. (2012貴州黔東南4分)計算cos60°= ▲ .
【答案】 。
【考點】特殊角的三角函數值。
【分析】直接根據記憶的內容得出結果:cos60°= 。
4. (2012貴州黔東南4分)用6根相同長度的木棒在空間中最多可搭成 ▲ 個正三角形.
【答案】4。
【考點】等邊三角形的性質。
【分析】用6根火柴棒搭成正四面體,四個面都是正三角形。故答案為4。
5. (2012貴州黔南5分)都勻市某新修“商業大廈”的一處自動扶梯如圖,已知扶梯的長l為10米,該自動扶梯到達的高度h為6米,自動扶梯與地面所成的角為θ,則tanθ的值等于 ▲ 。
【答案】 。
【考點】完全平方式。解直角三角形的應用(坡度坡角問題),勾股定理,銳角三角函數定義。
【分析】在由自動扶梯構成的直角三角形中,已知了坡面l和鉛直高度h的長,可用勾股定理求出坡面的水平寬度,進而求出θ的正切值:
如圖;在Rt△ABC中,AC=l=10米,BC=h=6米;
根據勾股定理,得:AB= (米)
∴tanθ= 。
6. (2012貴州黔西南3分)如圖,在梯形ABCD中,AD/pic/p>
【答案】27。
【考點】相似三角形的判定和性質。
【分析】先判定出△AOD∽△BOC,再根據相似三角形面積的比等于相似比的平方列式計算即可得解:
∵AD∥BC,∴△AOD∽△BOC。∴ 。
∵AD=1,BC=3, ,∴ 。
∴ 。
三、解答題
1. (2012貴州貴陽10分)小亮想知道亞洲最大的瀑布黃果樹夏季洪峰匯成巨瀑時的落差.如圖,他利用測角儀站在C處測得∠ACB=68°,再沿BC方向走80m到達D處,測得∠ADC=34°,求落差AB.(測角儀高度忽略不計,結果精確到1m)[來源:學科網ZXXK]
【答案】解:∵ACB=68°,∠D=34°,∠ACB是△ACD的外角,
∴∠CAD=∠ACB﹣∠D=68°﹣34°=34°。∴∠CAD=∠D。∴AC=CD=80。
在Rt△ABC中,AB=AC×sin68°≈80×0.927≈74(m)。
答:落差AB為74m。
【考點】解直角三角形的應用(仰角俯角問題),等腰三角形的判定,銳角三角函數定義。
【分析】根據三角形外角的性質求出∠CAD的度數,故可得出∠CAD=∠D,所以AC=CD=80,在Rt△ABC中,由AB=AC×sin68°即可得出結論。
2. (2012貴州安順10分)丁丁想在一個矩形材料中剪出如圖陰影所示的梯形,作為要制作的風箏的一個翅膀.請你根據圖中的數據幫丁丁計算出BE、CD的長度(精確到個位, ≈1.7).
【答案】解:由∠ABC=120°可得∠EBC=60°,
在Rt△BCE中,CE=51,∠EBC=60°,∴tan60°= 。
∴ (cm)。
在矩形AECF中,由∠BAD=45°,得∠ADF=∠DAF=45°,∴DF=AF=51。
∴FC=AE≈34+29=63,∴CD=FC﹣FD≈63﹣51=12(cm)。
∴BE的長度均為29cm,CD的長度均為12cm。
【考點】解直角三角形的應用,銳角三角函數定義,矩形的性質。
【分析】在Rt△BCE中,CE=51,∠EBC=60°,求得BE,在Rt△ADF中,由∠FAD=45°,從而求得DF=AF=51,從而求得BE,CD的長度。
3. (2012六盤水12)如圖,小麗想知道自家門前小河的寬度,于是她按以下辦法測出了如下數據:小麗在河岸邊選取點A,在點A的對岸選取一個參照點C,測得∠CAD=30°;小麗沿岸向前走30m選取點B,并測得∠CBD=60°.請根據以上數據,用你所學的數學知識,幫小麗計算小河的寬度.
【答案】解:如圖,過點C作CE⊥AD于點E,
由題意得,AB=30m,∠CAD=30°,∠CBD=60°,
∴∠ACB=∠CAB=30°。∴AB=BC=30m。
設BE=x,在Rt△BCE中,可得CE= x,
又∵BC2=BE2+CE2,即900=x2+3x2,
解得:x=15。∴CE=15 m。
答:小麗自家門前的小河的寬度為15 m。
【考點】解直角三角形的應用,勾股定理,銳角三角函數定義,特殊角的三角函數值。
【分析】根據題意畫出示意圖,過點C作CE⊥AD于點E,設BE=x,則在RT△ACE中,可得出CE,利用等腰三角形的性質可得出BC,繼而在RT△BCE中利用勾股定理可求出x的值,也可得出CE的長度。
4. (2012貴州黔東南12分)如圖,一艘貨輪在A處發現其北偏東45°方向有一海盜船,立即向位于正東方向B處的海警艦發出求救信號,并向海警艦靠攏,海警艦立即沿正西方向對貨輪實施救援,此時距貨輪200海里,并測得海盜船位于海警艦北偏西60°方向的C處.
(1)求海盜船所在C處距貨輪航線AB的距離.
(2)若貨輪以45海里/時的速度向A處沿正東方向海警艦靠攏,海盜以50海里/時的速度由C處沿正南方向對貨輪進行攔截,問海警艦的速度應為多少時才能搶在海盜之前去救貨輪?(結果保留根號)
【答案】解:(1)作CD⊥AB于點D,
在Rt△ADC中,∵∠CAD=45°,∴AD=CD。
在Rt△CDB中,∵∠CBD=30°,∴ =tan30°
∴BD= CD。
∵AD+BD=CD+ CD=200,∴CD=100( ﹣1)。
(2)∵海盜以50海里/時的速度由C處沿正南方向對貨輪進行攔截,
∴海盜到達D處用的時間為100( ﹣1)÷50=2( ﹣1)。
∴警艦的速度應為[200﹣100( ﹣1)]÷2( ﹣1)=50 (千米/時)。
【考點】解直角三角形的應用(方向角問題),銳角三角函數定義,特殊角的三角函數值。
【分析】(1)由條件可知△ABC為斜三角形,所以作AC上的高,轉化為兩個直角三角形求解。
(2)求得海盜船到達D處的時間,用BD的長度除以求得的時間即可得到結論。
5. (2012貴州銅仁10分)如圖,定義:在直角三角形ABC中,銳角α的鄰邊與對邊的比叫做角α的余切,記作ctanα,即ctanα= ,根據上述角的余切定義,解下列問題:
(1)ctan30°= ;
(2)如圖,已知tanA= ,其中∠A為銳角,試求ctanA的值.
6. (2012貴州遵義8分)為促進我市經濟的快速發展,加快道路建設,某高速公路建設工程中需修隧道AB,如圖,在山外一點C測得BC距離為200m,∠CAB=54°,∠CBA=30°,求隧道AB的長.(參考數據:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38, ≈1.73,精確到個位)
【答案】解:過點C作CD⊥AB于D,
∵BC=200m,∠CBA=30°,
∴在Rt△BCD中,CD= BC=100m,
BD=BC•cos30°=200× =100 ≈173.0(m)。
∵∠CAB=54°,
∴在Rt△ACD中, (m)。
∴AB=AD+BD≈173.0+73.5=246.5≈247(m)。
答:隧道AB的長為247m。
【考點】解直角三角形的應用,銳角三角函數定義,近似值。
【分析】構造直角三角形:過點C作CD⊥AB于D。在Rt△BCD中,利用三角函數的知識,求得BD,CD的長,從而在Rt△ACD中,利用∠CAB的正切求得AD的長,由AB=AD+BD求得答案。
【三角形貴州中考數學題及答案】相關文章:
圖形的變換貴州中考數學題匯總及答案12-17
統計與概率貴州中考數學題匯總09-15
平面幾何基礎貴州中考數學題匯總10-05
圓中考數學題匯總附答案02-15
中考模擬考試數學題及答案02-14
全等三角形中考模擬數學題匯總12-28
三角形之遼寧中考數學題匯總09-23
等邊三角形中考數學題匯總09-07
2016年貴州畢節中考語文試題及答案11-29