- 相關推薦
小學六年級數學教案：函數的對稱性與周期性
對稱性：函數圖象存在的一種對稱關系，包括點對稱和線對稱。
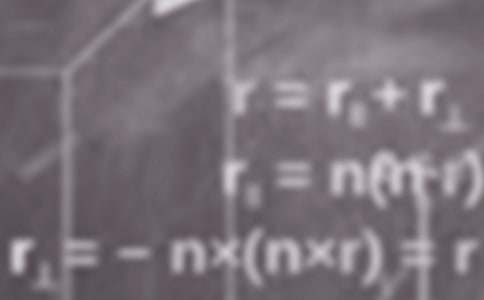
周期性：設函數 的定義域是 ，若存在非零常數 ，使得對任何 ，都有 且 ，則函數 為周期函數， 為 的一個周期。
對稱性和周期性是函數的兩大重要性質，他們之間是否存在著內在的聯系呢?本文就來研究一下它們之間的內在聯系，有不足之處望大家批評指正。
一、一個函數關于兩個點對稱。
命題1：如果函數 的圖象關于點 和點 對稱，那么函數 是周期函數， 為函數 的一個周期。
證明：∵函數 的圖象關于點 對稱，
對定義域內的所有 成立。
又∵函數 的圖象關于點 對稱，
對定義域內的所有 成立。
從而
即：
是周期函數， 為函數 的一個周期。
特例：當 時， 為奇函數，即奇函數 如果又關于點 對稱，那么函數 是周期函數， 為函數 的一個周期。
命題 ：如果函數 的圖象關于兩點 和 對稱，那么：
當 ， 時， 是周期函數， 為函數 的一個周期。
當 ， 時， 不是周期函數。
證明：∵函數 的圖象關于點 對稱，
對定義域內的所有 成立。
又∵函數 的圖象關于點 對稱，
對定義域內的所有 成立。
從而
當 ， 時
即：
當 ， 時， 是周期函數， 為函數 的一個周期。
當 ， 時
當 ， 時， 不是周期函數。
當 ， 時
(與條件矛盾，舍去)
綜合得原命題成立。
二、一個函數如果關于一個點和一條線對稱。
命題2：如果函數 的圖象關于點 和直線 對稱，那么函數 是周期函數， 為函數 的一個周期。
證明：∵函數 的圖象關于點 對稱，
對定義域內的所有 成立。
又∵函數 的圖象關于直線 對稱，
對定義域內的所有 成立。
從而
即：
即：
是周期函數， 為函數 的一個周期。
特例：當 時， 為奇函數，即奇函數 如果又關于直線 對稱，那么函數 是周期函數， 為函數 的一個周期。
命題 ：如果函數 的圖象關于點 和直線 對稱，那么函數 是周期函數， 為函數 的一個周期。
證明：∵函數 的圖象關于點 對稱，
對定義域內的所有 成立。
又∵函數 的圖象關于直線 對稱，
對定義域內的所有 成立。
從而
即：
即：
是周期函數， 為函數 的一個周期。
三、一個函數如果關于兩條線對稱。
命題3：如果函數 的圖象關于直線 和直線 對稱，那么函數 是以 為周期的周期函數。
證明：∵函數 的圖象關于直線 對稱，
對定義域內的所有 成立。
又∵函數 的圖象關于直線 對稱，
對定義域內的所有 成立。
從而
即：
是以 為周期的周期函數。
【小學六年級數學教案：函數的對稱性與周期性】相關文章：
關于《三角函數的周期性》的教案04-10
函數的數學教案04-18
函數數學教案05-10
數學教案：對數函數教案05-13
高一數學教案《函數》07-10
數學教案:函數單調性的應用05-16
高一數學教案《函數概念》06-04
數學教案：二次函數的圖象01-10
《反比例函數》初三數學教案02-13